Gray-Scott system of equations

Gray Scott U variable

We use the Gray-Scott as a simple reaction-diffusion 2 variable system of equations. The evolution of the variables are driven by a Laplacian operator, feed and kill concentration rates and a random source term in U.

\[\frac{∂U}{∂t} = D_U \cdot \left[ \frac{∂^2U}{∂x^2} + \frac{∂^2U}{∂y^2} + \frac{∂^2U}{∂z^2}\right] - U \cdot V^2 + F \cdot (1-U) + n \cdot r\] \[\frac{∂V}{∂t} = D_V \cdot \left[ \frac{∂^2V}{∂x^2} + \frac{∂^2U}{∂y^2} + \frac{∂^2U}{∂z^2}\right] + U \cdot V^2 - \left( F + k \right) \cdot V\]

where:

Outputs:

• \(U\) and \(V\) are the concentrations of two reacting and diffusing chemicals

Inputs:

• \(D_u\) and \(D_v\) are the respective diffusion rates
• \(F\) is the feed rate of \(U\) into the system
• \(k\) is the kill rate of \(V\) from the system
• \(n\) is the magnitude of the noise to be added to the system
• \(r\) is a normalized random number between -1 and 1

Discretization and 3D Stencil Solver

We just apply the classical finite difference method to the time \(t\) and spatial independent variables on a normalized \(\Delta\,x = \Delta\,y = \Delta\,z = 1\) three-dimensional (3D) grid mesh:

\[U_{t+1, i,j,k} = U_{t, i,j,k} + \Delta t \left [ D_U \cdot \nabla^2 U_{t,i,j,k} - U_{t,i,j,k} \cdot V_{t,i,j,k}^2 + F \cdot (1-U_{t,i,j,k}) + n \cdot r_{t,i,j,k} \right ]\] \[V_{t+1, i,j,k} = V_{t, i,j,k} + \Delta t \left [ D_V \cdot \nabla^2 V_{t,i,j,k} + U_{t,i,j,k} \cdot V_{t,i,j,k}^2 - \left ( F + k \right) \cdot V_{t,i,j,k} \right ]\]

where the Laplacian operator is defined for the 3D 7-point stencil in normalized spatial units:

\[\nabla^2 U_{t,i,j,k} = U_{t,i-1,j,k} + U_{t,i+1,j,k} + U_{t,i,j-1,k} + U_{t,i,j+1,k} + U_{t,i,j,k-1} + U_{t,i,j,k+1} - 6 \cdot U_{t,i,j,k}\]

where \(\Delta t\) is an input timestep variable.

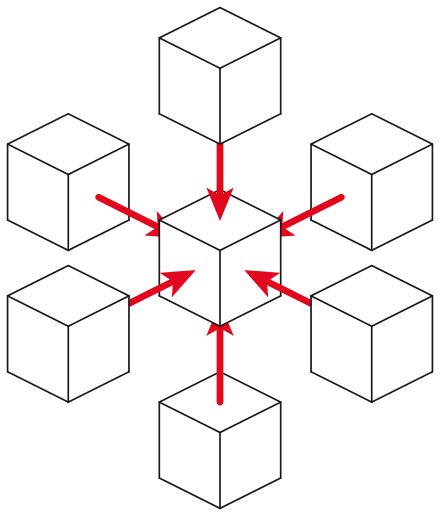3D 7-point stencil

Since each new timestep value for U and V only depends on neighboring values the problem is parallelizable on CPU and GPU providing an extra memory allocation for U and V field values.